第８回物理教室セミナー

日時：2005年1月22日(土)16時から

場所：23号館1階共用室

　自然界で見られるフラクタル図形（部分と全体が自己相似になっている図形、複雑さの程度はフラクタル次元によって表わされる）の具体的な例としては、枝分かれした樹木の形や海岸線の形があげられる。フラクタル幾何学の創始者であるB.B.Mandelbrotは、その著書「フラクタル幾何学」において、いくつかの実例を示している。例えば、ブリテン島の西海岸のフラクタル次元Dは1.3となっている。

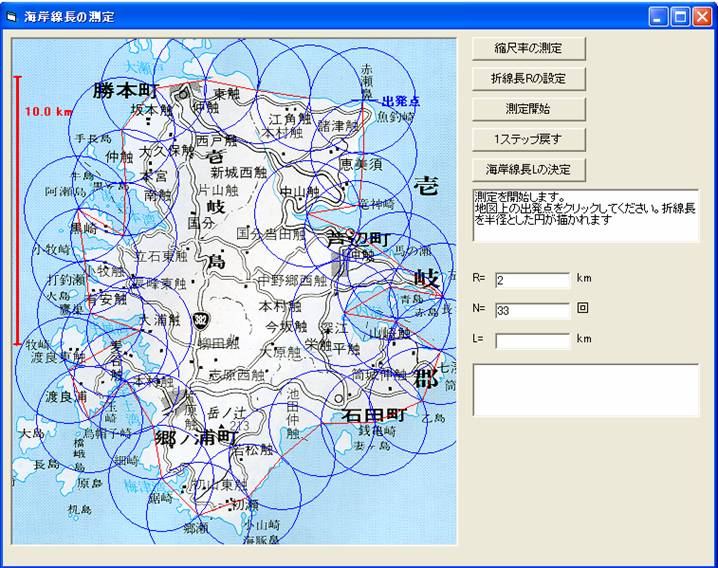
　ここでは、海岸線の長さをディバイダー法で測定するコンピューター･シミュレーション・プログラムを紹介する。その応用として、いくつかの海岸線のフラクタル次元を求める。

　ディバイダー法は、開きRのディバイダーを当てて海岸線の長さLを測る。Rを小さくすると、Lは大きくなる。横軸にlog Rを、縦軸にlog Lをとって測定点をプロットし、測定点を結ぶ直線の勾配を求める。フラクタル次元Dは、D＝１- (直線の勾配) によって決定される。　担当：鎌倉 史郎